Distribución Normal: Ejercicios

Que tal!

A continuación veremos unos ejercicios resueltos mediante Distribución normal:

Gracias!
Comparte!

Distribución Poisson

El dia de hoy tendremos una entrada sobre la Distribución Poisson, la cual es una de las más importantes distribuciones de variable discreta. Sus principales aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o de espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias restrictivas. Otro de sus usos frecuentes es la consideración límite de procesos dicotómicos reiterados un gran número de veces si la probabilidad de obtener un éxito es muy pequeña .  

-Proceso experimental del que se puede hacer derivar

   - Esta distribución se puede hacer derivar de un proceso experimental de observación en el que tengamos las siguientes características

· Se observa la realización de hechos de cierto tipo durante un cierto periodo de tiempo o a lo largo de un espacio de observación

· Los hechos a observar tienen naturaleza aleatoria ; pueden producirse o no de una manera no determinística.

· La probabilidad de que se produzcan un número x de éxitos en un intervalo de amplitud t no depende del origen del intervalo (Aunque, sí de su amplitud)

· La probabilidad de que ocurra un hecho en un intervalo infinitésimo es prácticamente proporcional a la amplitud del intervalo.

· La probabilidad de que se produzcan 2 o más hechos en un intervalo infinitésimo es un infinitésimo de orden superior a dos.

En consecuencia, en un intervalo infinitésimo podrán producirse O ó 1 hecho pero nunca más de uno

· Si en estas circunstancias aleatorizamos de forma que la variable aleatoria X signifique o designe el "número de hechos que se producen en un intervalo de tiempo o de espacio", la variable X se distribuye con una distribución de parámetro l . Así :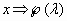           

    El parámetro de la distribución es, en principio, el factor de proporcionalidad para la probabilidad de un hecho en un intervalo infinitésimo. Se le suele designar como parámetro de intensidad , aunque más tarde veremos que se corresponde con el número medio de hechos que cabe esperar que se produzcan en un intervalo unitario (media de la distribución); y que también coincide con la varianza de la distribución.

    Por otro lado es evidente que se trata de un modelo discreto y que el campo de variación de la variable será el conjunto de los número naturales, incluido el cero:    
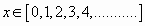Que sería :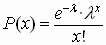         

A continuación unos problemas que se resolvieron por medio de excel!

Distribución Binomial

Una distribución binomial o de Bernoulli tiene las siguientes características:

1. En cada prueba del experimento sólo son posibles dos resultados: éxito y fracaso.
2.La probabilidad de éxito es constante, es decir, que no varía de una prueba a otra. Se representa por p.
3.La probabilidad de fracaso también es constante, Se representa por q = 1 − p
3.El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
5.La variable aleatoria binomial, X, expresa el número de éxitos obtenidos en las n pruebas. Por tanto, los valores que puede tomar X son: 0, 1, 2, 3, 4, ..., n.

La distribución bimomial se expresa por B(n, p)

La formula es la siguiente

n= es el numero de pruebas
k= el numero de exitos
p= probabilidad de exito
q=probabilidad de fracaso

 
Esta formula la usamos para sustituir el valor de (n/k)

Pero no hay mejor manera de comprender algo que poniéndolo en práctica, es por esto que a continuación se trabaja lo ya visto en algunos ejercicios: 

Gracias por tu visita!
Ayúdame compartiendo!